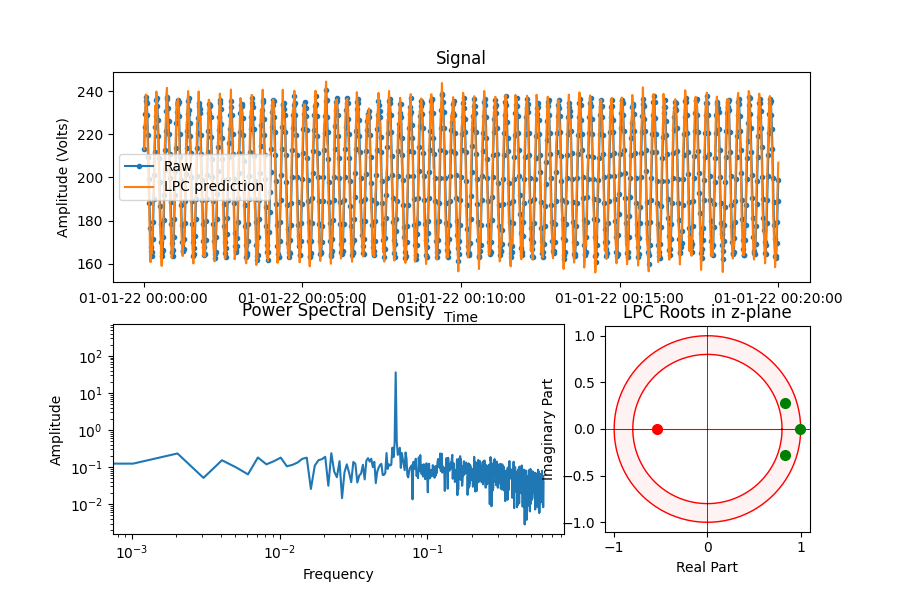
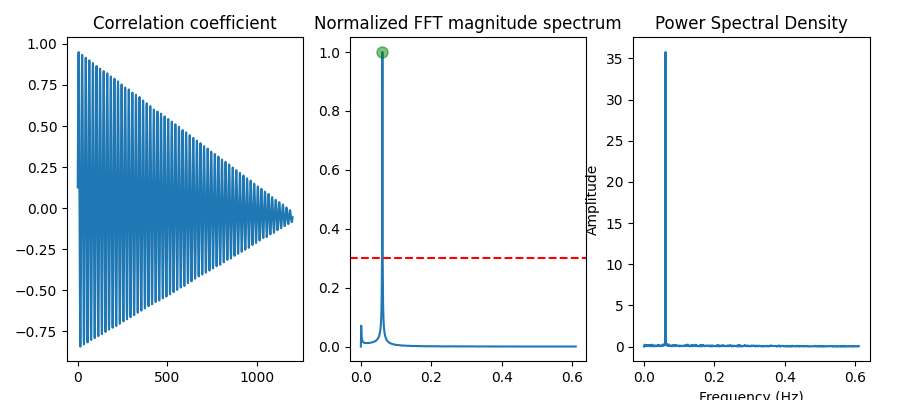
Oscillation detection using linear predictive coding

Identifies if a signal contains one or more oscillatory components. Based on the paper by Sharma et. al. [#]_.

• 
• 
• 

/Users/neringaaltanaite/Project/indsl/indsl/detect/oscillation_detector.py:580: UserWarning: The figure layout has changed to tight
  fig.tight_layout()

import os

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

from indsl.detect.oscillation_detector import helper_oscillation_detector, oscillation_detector


# brownian noise wave signal
base_path = "" if __name__ == "__main__" else os.path.dirname(__file__)
data = pd.read_csv(os.path.join(base_path, "../../datasets/data/brownian_noise_wave.csv"), index_col=0).squeeze(
    "columns"
)

# convert str to datetime
data.index = pd.to_datetime(data.index)

# call oscillation detector function
results = oscillation_detector(data)

# output dictionary
dict_output = helper_oscillation_detector(data)

# plot the results
fig, ax = plt.subplots(1, 1, figsize=[10, 5])

ax.plot(
    results.index,
    results.values,
    color="blue",
    linestyle="dashed",
    linewidth=1,
    markersize=1,
    marker=".",
)

ax.set_xlabel("freq (Hz)")
ax.set_ylabel("detection (1: detected, 0: no detection)")
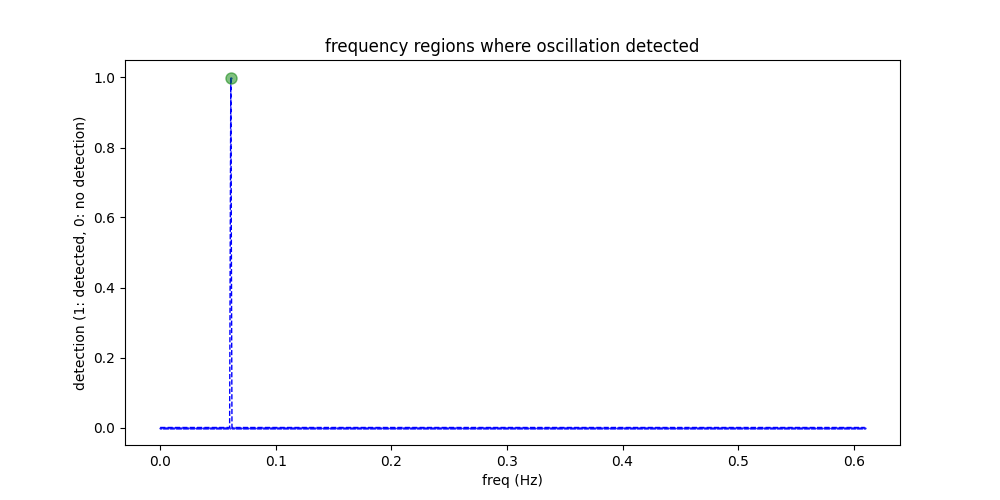
ax.set_title("frequency regions where oscillation detected")
ax.plot(results.index[np.where(results.values == 1)], 1, "go", markersize=8, alpha=0.5)

plt.show()